Friends

I just read an article in an old The Helix magazine that said: on average your friends have more friends than you do.

It is true, and maybe even obvious to some people, but I thought I'd have a go at modelling it. 

Firstly, I'm thinking the log normal distribution is a good estimation of how many friends people have. It is a one parameter family based on the standard deviation σ of the normal distribution that it is the log of. 

I use log normal because nobody has a negative number of friends, and a few people have hundreds or thousands of friends. So it is a skewed distribution. It isn't a Poisson distribution though because the tail isn't that thick. Here is the log normal distribution shown for σ = 0.5:

Note that the horizontal scale is arbitrary, the peak above could represent 1 friend or 100 friends.

The mean of a log normal distribution is exp(σ^2 / 2)

To see the distribution of your friend's friends you need to multiply the log normal PDF by x, because the more friends the person has (larger x) the more likely you are to be friends with them. 

The mean of this distribution is exp(3 * σ^2 / 2). σ^2 being the variance. 

The ratio of these two means represents how many more friends your friends have than you do. This is simply exp(σ^2):

This value depends a lot on the unknown parameter σ. If we have a diverse number of friends then it will potentially be very large, starting to grow rapidly for σ > 1.

Either way, the ratio is always > 1 so this model supports the claim. 

The magazine cited Facebook data that 85% of people's friends have more friends than them. Presumably one could work backwards to estimate σ for this case. But σ=0.5 looks like a reasonable distribution for number of real friends, and that gives your friends 28% more friends than you have. 

For a wider range σ=1 your friends have e times as many friends as you do!

Inversion Table

I have been working on extending the previous inversion shapes into a full table of inversion fractals. It does appear that spherical inversion is a nice way to get 'canonical' examples of each recursive shape described in the classification table here.

I have used Shadertoy with a simple render path here.

In addition to the already discussed sphere cluster, there are two main methods worth discussion:

1. Trees

I have used a different method to the previous inversion trees. Instead, I have taken a platonic solid (currently only tetrahedron, octahedron and cube) and places a sphere inversion at each face to generate the domes, and a sphere inversion at each corner to generate the intermediate domes between the hemispherical large domes. 

There is therefore a parameter to control the doming angle and a second parameter to control the width of this intermediate area. 

Above is a tree using the octahedron platonic solid, so there are 8 large domes on the octahedron faces and a 'cross' structure filling the gap between those domes. 

The doming angle can be increased to generate a tree-sponge and then to generate a sponge-sponge:

Also, the doming angle can be made negative to generate a shell-shell (recursive indentations):

We can even alternate the doming angle to generate a shell-tree, so it is quite a versatile method for generating various classes of recursive shape.

2. Clusters

In addition to the already described sphere cluster (which I use for the cluster-cluster class), we can generate recursive shapes on platonic solids by placing contacting spheres at each face, with a central contacting sphere in the middle. This is currently just done for tetrahedron, octahedron and cube, just like the tree structures above.

If each sphere recurses to the central sphere, then it generates a void-sponge:

If we make the outer spheres smaller so that they contact the central sphere but not themselves then it makes a void-tree:

and if we make them smaller so that they don't touch the central sphere either, then it generates a void-cluster:

In each case, the platonic solid can be chosen, as can the relative sphere sizes. 

In addition to these void (pure fractal) objects, the recursion method can be applied to any bounded shape to make a cluster of those shapes. So for instance, we can make a shell-cluster:

These two broad methods provide most of the 16 classes that I have so far generated. These are selected by clicking on the appropriate square in the table grid that overlays the fractal (as seen in the above images). There are a couple of outlier types that I have also added:

void-foam

This is simply a sphere-packing using a Kleinian group similar to the Gx series but in 3D.

cluster-foam

This is a special version of the Kleinian group that includes solid areas.

foam-cluster

This is a modification of the cluster-cluster previously described, which esentially inverts the cluster-cluster around its sphere, to give a foam structure on the inside. This is done recursively, so the empty spheres in the foam also have little sphere clusters inside them. 

Remainder:

The remaining shapes are principally shells and sponge structures. I am not yet sure how best to make these with sphere inversions. Any suggestions are appreciated.

Void Cluster

Fractal dust AKA a void-cluster is fairly easy to generate, for example the 3D Cantor dust. Here I continue working on developing less rectilinear examples by using sphere inversion.

The method I use is very similar to the previous Sphere Cluster in that it uses the dodecahedral or icosahedral symmetries together with the offset sphere inversion that typically generates the hyperbolic tesselation of the above polyhedrons.

The difference is with this void-cluster we do not apply the centralised sphere inversion when recursing into a sub-cluster, and we rescale the cluster from rk up to 1 each iteration unconditionally.

The result is an icosahedral/dodecahedral set of sub-clusters, together with the rk sized subcluster in the centre. Here for k=0.9:

Above left: icosahedral and right dodecahedral void-clusters

Above: same but alternating between the two types 

Here are the same variations for k=1 from an approximately symmetrical view angle:

The problem with these clusters is only that they don't seem to be a proper generalisation of the Sphere Cluster, becaue they aren't based on an inversion of a regular polyhedral tesselation.

Any hyperbolic tesselation when inverted will give a central sphere of finite size, leading to the Sphere Cluster when applied recursively. If you think of the reducing radius central sphere as equivalent to a growing radius hyperbolic disk, then the limit would be an infinite radius (and zero curvature) hyperbolic disk which is flat Euclidan space. The only regular polyhedral teselation of Euclidean space is cubic. 

So we invert the space, then pull all cubes in the tesselation into the central cube. This is the equivalent of the multiple dot products and offset sphere inversions in the Sphere Cluster. Then shrink the space by k and recurse.

The result for k from 0.4 up to 1.6 is:

 The significant points along the way are k=1 where it goes from a void-cluster to a void-sponge:

and k=2 where (despite rendering artifacts) it becomes a void-foam:

(slice-through visible).

This is a very interesting family of shapes as it covers three fractal classes, and it seems to be a generalisation of the Sphere Cluster (which itself seems to cover cluster, cluster-sponge and possible cluster-foam classes). But more interesting is that even the finest k=0.4 case seems like its fractal dimension would be 3, due to being the inversion of a 3D (cubic) lattice.

Here's a higher detail of k=0.5:

Inversion Tree

 A while ago I wrote about three variable-dimension surfaces, which included a sphere inversion-based surface. The idea is to use a disk packing and then convert each disk into a spherical bulge and repeat. 

At the time I only knew about the Apollonian Gasket sort of disk packings, and these have the problem that finite sized disks touch each other, so if you keep adding bulges then the surface will self-intersect. For this reason I chose a type of packing where I could toggle the direction to prevent intersections. But the result is not a tree for this reason. 

If we instead make use of Kleinian packings such as the G8 packing, then finit disks don't butt up against each other, and the disk radii drop relatively uniformly with distance to the disk edge. It is therefore possible convert them all into spherical bulges without self-intersection. 

The method follows that in the Kajino paper but with a bigger family of disk packings. Here the G8 group example is used, like in my recent post:

The left image is the limit set and the right shows the three symmetries used to generated it. These are defined by the three green lines (exactly as used previously) and the purple L4 line. To see if a point is in the set, repeatedly:

1. reflect around the two straight lines until the point is within that wedge

2. if the point is inside the l2 circle then invert around that circle

3. if the point is inside the l4 circle then revert around that circle

4. if the point is outside the centred green circle then colour white and exit

colour black if iterations ended

Notice that these transformations never make the space (close clusters of points) smaller, so this is a form of escape-time fractal. If we use the l2,l4 labels for the two circle radii and the letter L for the distance of l4's centre from the origin then:

- l2 = sec(pi/o1) / sqrt(cosec^2(pi/n) - sec^2(pi/o1))

- L = sqrt(1+l2^2)

- l4 = L sin(pi/o2 - asin(l2 sin(pi-pi/o2)/L)/sin(pi - pi/o2)

Where n is the number of child disks to the central one, and o1 and and o2 are two different order numbers, in particular, o1 is the number of hyperbolic tesselation regular polygons that meet at each vertex.

While all produce types of Kleinian group, it so happens that the types that I want (no bald spots, no black disks) happen when o2=3 and when o1 is the smallest value that is hyperbolic. For example if n=6 then three regular hexagons meeting at each vertex is a Euclidean tiling, so you need o1=4. For n from 4 up to 9 the values of o1 are therefore 5,4,4,3,3,3 respectively. The resulting tilings are shown in reading order here:

Hopefully you can see the number of children around the central disk grows from 4 up to 9, and that no two (finite sized) disks ever butt up against each other. You may also notice that the central disk size doesn't grow in a simple way with n, that is because o1 is changing, only remaining constant on the bottom row.

In order to render this as a tree of bulging disks we need to develop an approximate distance estimator. The method I use per iteration is as follows:

1. if the point is outside some spherical region above the disk then return the distance to a slightly smaller spherical region (scaled by the running scale). This is heuristic so takes some tuning.

2. apply the above escape-time transformations for limit set as a horizontal unit disk, but make sure that sphere inversions are 3D. 

3. if the point is within a sphere that encompasses the central disk, then apply a conformal transformation that bends the desired spherical bulge back to a flat disk, and scales it back to the unit disk.

if iterations run out then return the distance to the flat disk (scaled by the running scale).

This 'desired spherical bulge' is specified by a bend angle parameter which describes how much the bulge lifts up relative to being flat. We therefore are left with a tree family defined by two parameters: n and bendAngle.

Here is n=8 at bendAngle 0.3 up to 1.3 in steps of 0.2:

And here is bendAngle 1 for values of n from 4 up to 9, in reading order:

As with the 2D images above, there isn't a simple progression of the shape because o1 is changing, but the shape is largely governed by how large the central disk is.

As you can see, it not only generates a tree, but for large enough bendAngle it generates a tree-sponge when the branches touch, and then a sponge for higher bendAngle. It almost certainly then generates a foam structure at larger bend angles, but the distance estimator gets challenging to develop at these large angles.

We can look at just the inner disk shape, which is equivalent to applying the curve on the outer disk, here are some examples:

n=7

n=5

n=8

n=4

n=8

n=6

n=6

n=8

For the large bend angles producing a sponge, you need to tweak the bend angle to get a Kleinian group (circles are circles) rather than a pseudo-Kleinian (partial-circles), the above image has bend angle 1.26 to achieve this.

Sphere Cluster

We can generate 3D clusters in a similar way to the previous post, but using a hyperbolic regular polyhedron tiling instead of a hyperbolic regular polygon tiling. We can continue to use this 2D diagram as a guide:

We define the outer green circle as radius 1, and the offset green circle l2 has its centre at a distance L=sqrt(1+R^2) where R is the solution to:

 R/theta = sqrt(1+R^2)/sin(pi/2 + pi/m)

where theta is the angle from the polyhedron centre to the nearest face edge and m is the number of polyhedrons that meet at each edge. There are two good polyhedrons to use here, the dodecahedron and the icosahedron, their values and resulting formula are: 

 Dodecahedron: 

• theta = atan2(phi+2, 2phi + 2 + 1/phi)
• m      = 4
• R      = sqrt(2)/sqrt(-2 + cosec^2(theta))

Icosahedron:

• theta = atan2(phi, 1+2phi)
• m      = 3
• R      = 2/sqrt(-4 + cosec^2(theta))

Where phi is the golden ratio, and the inner red circle has radius r=L-R.

To render in 3D we want to do something better than just an inside-outside test, we want to approximate the distance to the nearest surface. It goes roughly like this... invert each query point p around the red radius r sphere then:

1. rotate the point to a be radially in one single polyhedron face*
2. if it is inside l2 you invert it around l2
3. if its magnitude is less than rk (plus a skin width) then divide by rk and then invert around l4 = sqrt(r), sending the red sphere to the outer green unit sphere
4. once you are out of iterations return the distance to the centre sphere rk, multiplier by a scale factor that is initialised to 1 and grows in proportion to all transformations of p in the above steps

* this is a bit harder in 3D than 2D. The simplest I can think of is to fold the point around the planes defined by the origin and each edge of the chosen face. For the dodecahedron the chosen face has vertices in order: (1/phi,0,phi), (1,-1,1), (phi, -1/phi,0), (phi,1/phi,0), (1,1,1). For the icosahedron the three vertices are (0,1,phi), (0,1,-phi), (phi,0,1). The planes can be generated using the cross product of adjacent vertices. I found that for the dodecahedron you just need to fold around each edge twice to guarantee the point ends up radially in the specified face, and for the icosahedron you need to do it three times. 

The direction to the l2 sphere centre is then the direction to this face centre, which is the mean of the above vertices.

The resulting approximate signed distance function to the shape's surface is sampled in Fragmentarium in order to generate a rendering of the shape with lighting and shadows. 

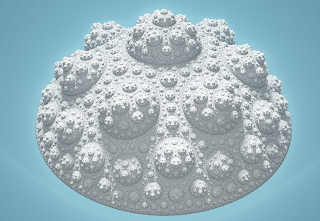
Here is the result for the dodecahedral cluster, with k values from 0.7 up to 1:

Here against a black background, a close up of k=0.7:

and k=0.8:

and k=0.1:

For the icosahedral cluster, here are k values of 0.7 up to 1:

Both the decahedral and the icosahedral become cluster-sponges at k=1, and are very spikey and visually less rough. We can make the shape less spikey at higher k by alternating between the dodecahedral and the icosahedral clusters. Since they are duals of each other, we should expect that to do the opposite of lining up subclusters. 

There are two versions depending on which shape you start with. Here starting with the dodecahedral with k from 0.8 up to 1:

a close up at k=1:

Here we start with the icosahedral shape, k = 0.7 to 1:

It is a bit hard to render this fractal for k>=1, but if you replace the final distance calculation with a slightly smaller sphere distance then it makes no difference to the limit set, and avoids some rendering artifacts for k>1, which is when the shape changes from a cluster to a sponge.

So here is the icosahedral fractal for k=1 and k=1.3:

and the dodecahedral from k=1 up to k=1.6:

If you toggle between icosahedral and dodecahedral, it is a bit more organic looking:

k=1.1 starting dodecahedral:

k=1.2

Starting icosahedral, k=1.1:

k=1.16

k=1.17