dimension-aware rasterising

How do you raster geometry? i.e. convert shapes to screen pixels. It might seem like that is a question solved many decades ago but maybe not...

Lets take a simple example of a disk (a filled in circle) which is just black against a white background. To render it we just need to set each pixel to black which is inside the circle right?
Well that is kind of true but not very accurate since we get jagged looking edges. The most accurate rendering would set the blackness of each pixel to the percentage of that pixel which is inside the disk. This gives a slight gradient along the edge which is smoother, it is sometimes called anti-aliasing:

You can see that the left disk looks better than the right disk, it is in fact the best rendering for this piece of geometry. The blackness is proportional to the area of the pixel that is inside the set.

This is in fact how most 2d geometry is rendered, for more complicated shapes it is usually achieved by supersampling, which means testing multiple points inside each pixel (e.g. a 4x4 grid of points) and averaging. This is an approximation of the ideal render since it is an approximation of the area under the pixel that is in the set. It gets closer to perfect as you increase the number of supersamples.

And that's where most rasterisers leave the issue of rastering. But there's a problem, how do you raster a line? You can't calculate the area under a pixel that contains the line because lines don't have area. You could solve the problem by saying that such 'thin' lines are invisible and so you render lines only by giving them a certain width. However this requires choosing a width and it is altering the object to a different shape. We should be entitled to see lines and points and other mathematical objects on our screen, even if they have no area.

In fact you can raster a line on screen, the ideal raster darkens each pixel in proportion to the length of line under that pixel, rather than the area, as seen in the lower line here:

Fine, but what about points? Points neither have area or length. The ideal rasteriser would darken each pixel based on the number of points under the pixel.

And what about rough objects like the Koch curve, this has neither length nor area but somewhere in between, in fact it is a 1.26 dimensional object, but that value depends upon its bend angle.

So rasterising geometry is starting to look very complicated..

Solution

In fact there is a single solution to all these cases, if you know the dimension of the geometry then you measure the 'amount' of geometry under each pixel in units of that dimension. So for the disk you measure the amount under the pixel in pixelWidth^2, for the line you measure the amount in pixelWidth^1, for the point the amount in pixelWidth^0 and for the Koch curve the amount in pixelWidth^1.26 etc. You then darken each pixel in proportion to this 'amount' (The Hausdorff measure). A single method for any dimensional object.

For more general shapes where the dimension isn't necessarily known or uniform we can approximate this ideal rasteriser by using supersampling. For each pixel you count the number of sub-pixels in the set at your maximum resolution (e.g. 4x4 for each pixel) c then you also count the number of sub-pixels containing the set at half that resolution (e.g. 2x2) h. The dimension is then calculated as d = log(c/h)/log(2) and the amount by which you darken the pixel is c/r^d where r is the supersample resolution, e.g. 4 in this example.

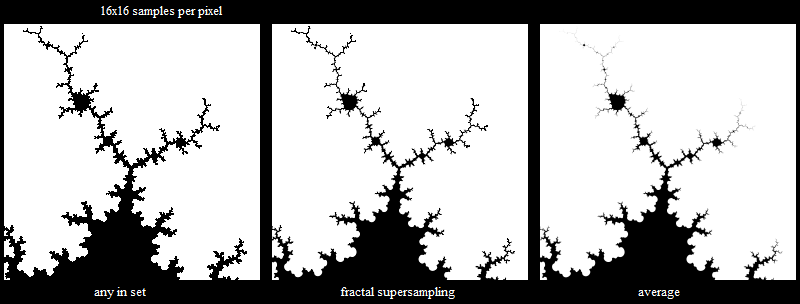
Here is the method applied to the Mandelbrot set. Even though the border has dimension 2, the set itself has various geometry of different dimensions within different scale ranges. e.g. there are crooked lines which might have dimension about 1.2 like the Koch curve, and solid areas with dimension 2:

The left image blackens each pixel if any of the 16x16 supersample points are in the set. It has no anti-aliasing and no smoothness even though the curves at the base should be smooth (since I'm only doing 20 Mandelbrot iterations).

The right image is averaging the 16x16 supersample points, it gives smooth curves at the base which is correct, but the line areas at the top fade out and you can't even see the geometry at the very top.

The centre image is using the new method. The base curves are smooth and the line areas at the top are all clearly visible as well as being anti-aliased.

I am using a fractal above as an easy way to get complex geometry, but the technique can work on any black and white image. Possibly it could be extended to colour images too, as a way to retain the important information in an image when sampling to a lower resolution. 

Here's a close up of the above image so you can see the antialiasing:

Here I shade the pixels based on the dimension at that point, viewing part of the Mandelbrot set at 20 and 2000 iterations. You can see the dimension reduces (gets lighter) further up the branch.

This image shows how you could use dimension-aware rasterising to get useful detail out of downsampled images, in this case showing power lines: