A useful result of mapping complex numbers to the Riemann sphere is that elementary functions like z^2 and z^3 can be interpreted geometrically.
z^2 wraps the sphere around onto itself, take the one faced spherical polyhedron shown above, cut it along the shown arc and stretch it around itself, as if doubling the longitude coordinates, until you can sew it back up at the original cut. The space naturally pinches toward the two poles such that the transform remains conformal. This is z^2.
Similary, z^3 takes the two-faced spherical polyhedron and wraps it around onto itself, as if stretching the complex plane by tripling the longitude around for example the Greenwich meridian.
z^4 wraps a three-faced spherical polyhedron onto itself, and z^5 wraps a four-faced spherical polyhedron onto itself. These shapes are all called hosohedra.
Given this interpretation, it is interesting to consider mappings that wrap other spherical polyhedra onto themselves. Afterall, while the first two example hosohedra are regular, the three and four faced ones are not. The four faced hosohedra is also an unstable partition of the sphere in some senses, the stable and regular four faced spherical polyhedron is a spherical tetrahedron:
So it is interesting that you can indeed wrap a spherical tetrahedron onto itself, and it does remain conformal. The function is this:
If the complex plane origin is point D in the above image then the constants in the numerator of the product are the vertices A,B and C. The constants in the denominator are the poles which map to the centre of the spherical triangle ABC, they are located at the centre of the three remaining spherical triangles.
The mapping can be visualised on the complex plane using David Bau's complex function viewer:
The grey circles are the unit disk in the complex plane, so you can see that this function can equally be seen to map a two sided spherical polyhedra (the the edge being the unit disk) to a spherical octahedron.
This animation I made shows the fold as applied to a non-spherical tetrahedron:
This tetrahedral wrapping function, for which I'll use the letter tau, can be simplified slightly if we allow it to wrap onto its dual tetrahedron (so removing the minus sign) and rearrange slightly to:
I find the look of this fractal to be quite different to others, even though you can clearly see mandelbrot elements within it. Here are two more close ups of the holes:
and here is part of the negative tau version:
which was rendered using Fragmentarium.
Dihedral version
While the above function is I think quite unique as a regular polyhedron that wraps onto itself, it is also possible to do so with a two-sided spherical polyhedron called a Dihedron {4,2} (which means four vertices and two faces):
The wrap is similar to taking a square (with two sides, like an envelope) and folding in half then in half again to form a smaller square, but in our case it is done on the inflated/spherical surface.
The function is:
Which can be visualised here. You can visualise the mandelbrot set of it by using its reciprocal:
Wow, these are great pics.. and the negative version:
It also produces a mandelbulb which has some similarities to the tetrahedral version:







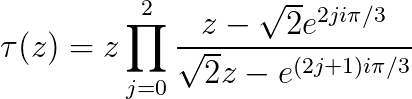.png)














No comments:
Post a Comment