Inversion Tree

 A while ago I wrote about three variable-dimension surfaces, which included a sphere inversion-based surface. The idea is to use a disk packing and then convert each disk into a spherical bulge and repeat. 

At the time I only knew about the Apollonian Gasket sort of disk packings, and these have the problem that finite sized disks touch each other, so if you keep adding bulges then the surface will self-intersect. For this reason I chose a type of packing where I could toggle the direction to prevent intersections. But the result is not a tree for this reason. 

If we instead make use of Kleinian packings such as the G8 packing, then finit disks don't butt up against each other, and the disk radii drop relatively uniformly with distance to the disk edge. It is therefore possible convert them all into spherical bulges without self-intersection. 

The method follows that in the Kajino paper but with a bigger family of disk packings. Here the G8 group example is used, like in my recent post:

The left image is the limit set and the right shows the three symmetries used to generated it. These are defined by the three green lines (exactly as used previously) and the purple L4 line. To see if a point is in the set, repeatedly:

1. reflect around the two straight lines until the point is within that wedge

2. if the point is inside the l2 circle then invert around that circle

3. if the point is inside the l4 circle then revert around that circle

4. if the point is outside the centred green circle then colour white and exit

colour black if iterations ended

Notice that these transformations never make the space (close clusters of points) smaller, so this is a form of escape-time fractal. If we use the l2,l4 labels for the two circle radii and the letter L for the distance of l4's centre from the origin then:

- l2 = sec(pi/o1) / sqrt(cosec^2(pi/n) - sec^2(pi/o1))

- L = sqrt(1+l2^2)

- l4 = L sin(pi/o2 - asin(l2 sin(pi-pi/o2)/L)/sin(pi - pi/o2)

Where n is the number of child disks to the central one, and o1 and and o2 are two different order numbers, in particular, o1 is the number of hyperbolic tesselation regular polygons that meet at each vertex.

While all produce types of Kleinian group, it so happens that the types that I want (no bald spots, no black disks) happen when o2=3 and when o1 is the smallest value that is hyperbolic. For example if n=6 then three regular hexagons meeting at each vertex is a Euclidean tiling, so you need o1=4. For n from 4 up to 9 the values of o1 are therefore 5,4,4,3,3,3 respectively. The resulting tilings are shown in reading order here:

Hopefully you can see the number of children around the central disk grows from 4 up to 9, and that no two (finite sized) disks ever butt up against each other. You may also notice that the central disk size doesn't grow in a simple way with n, that is because o1 is changing, only remaining constant on the bottom row.

In order to render this as a tree of bulging disks we need to develop an approximate distance estimator. The method I use per iteration is as follows:

1. if the point is outside some spherical region above the disk then return the distance to a slightly smaller spherical region (scaled by the running scale). This is heuristic so takes some tuning.

2. apply the above escape-time transformations for limit set as a horizontal unit disk, but make sure that sphere inversions are 3D. 

3. if the point is within a sphere that encompasses the central disk, then apply a conformal transformation that bends the desired spherical bulge back to a flat disk, and scales it back to the unit disk.

if iterations run out then return the distance to the flat disk (scaled by the running scale).

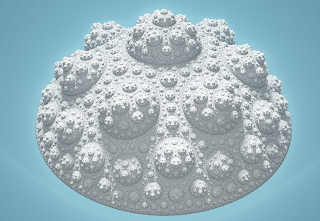
This 'desired spherical bulge' is specified by a bend angle parameter which describes how much the bulge lifts up relative to being flat. We therefore are left with a tree family defined by two parameters: n and bendAngle.

Here is n=8 at bendAngle 0.3 up to 1.3 in steps of 0.2:

And here is bendAngle 1 for values of n from 4 up to 9, in reading order:

As with the 2D images above, there isn't a simple progression of the shape because o1 is changing, but the shape is largely governed by how large the central disk is.

As you can see, it not only generates a tree, but for large enough bendAngle it generates a tree-sponge when the branches touch, and then a sponge for higher bendAngle. It almost certainly then generates a foam structure at larger bend angles, but the distance estimator gets challenging to develop at these large angles.

We can look at just the inner disk shape, which is equivalent to applying the curve on the outer disk, here are some examples:

n=7

n=5

n=8

n=4

n=8

n=6

n=6

n=8

For the large bend angles producing a sponge, you need to tweak the bend angle to get a Kleinian group (circles are circles) rather than a pseudo-Kleinian (partial-circles), the above image has bend angle 1.26 to achieve this.